- the grid is filled with a unique facies
- the porosity is defined in 5 different layers
- the fluid is initiated froma single cell located at the upper right corner of the grid
- Code: Select all
nx = 300
ny = 200
grid = db.create(nx=c(nx,ny))
table = data.frame(x1=c(50,150,200,250,50,150,200,250,50,150,250),
x2=c(150,120,100,125,100,90,85,100,50,60,50),
z1=c(1,1,1,1,2,2,2,2,3,3,3))
db = db.create(table)
The first part consists in defining the contents of the grid by simulating several layers. For that sake, we perform an estimation (based on Kriging) and connditioned by a small set of samples: A set of limits is also prepared which will be used to subdivide the grid into several layers.
- Code: Select all
model = model.create("Cubic",range=100)
neigh = neigh.create(ndim=2,type=0)
grid = kriging(dbin=db,dbout=grid,model=model,neigh=neigh,uc=c("1","y"),flag.std=FALSE)
grid = db.rename(grid,4,"L")
limits = limits.input(5,flag.regular=T)
Now we calculate the porosity for each layer. This will be done by setting or simulating the log-porosity.
For the first layer, we consider that. the log-porosity is constant and equal to 1 (variable m1)
- Code: Select all
grid = db.add(grid,m1=1)
For the second layer, the log-porosity is simulated using an isotropic exponential structure with range equal to 50 (variable m2)
- Code: Select all
grid = simtub(dbout=grid,model=model.create(vartype="Exponential",range=50))
grid = db.rename(grid,6,"m2")
For the third layer, the log-porosity is simulated using an anisotropic exponential structure with a range of 200 along X and 100 along Y (variable m3)
- Code: Select all
grid = simtub(dbout=grid,model=model.create(vartype="Exponential",range=c(100,200)))
grid = db.rename(grid,7,"m3")
For the fourth layer, the log-porosity is simulated using an anisotropic gaussian structure with a range of 400 in N30 and 100 in the orthogonal direction (variable m4)
- Code: Select all
grid = simtub(dbout=grid,model=model.create(vartype="Gaussian",range=c(20,80),aniso.rotmat=util.ang2mat(ndim=2,angles=30)))
grid = db.rename(grid,8,"m4")
Finally for the fifth layer, the log-porosity is simulated using an anisotpric cubic structure with a range of 400 in N-30 and 100 in the orthogonal direction (variable m5)
- Code: Select all
grid = simtub(dbout=grid,model=model.create(vartype="Cubic",range=c(50,200),aniso.rotmat=util.ang2mat(ndim=2,angles=-30)))
grid = db.rename(grid,9,"m5")
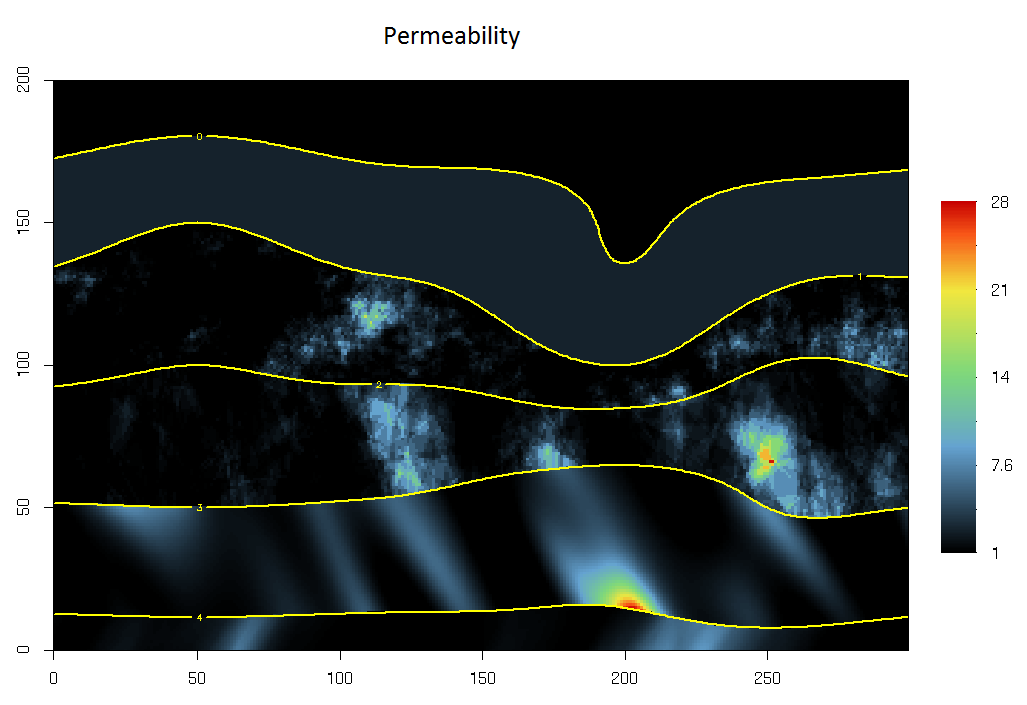
Finally all the log-porosity variables are transformed into porosities. The variable "Layers" is then used to create indicator variables. Combining the porosity and indicator variables leads to the new Porosity variable. Finally the spurious construction variables are cleaned out.
- Code: Select all
grid = db.add(grid,m1e=exp(m1))
grid = db.add(grid,m2e=exp(m2))
grid = db.add(grid,m3e=exp(m3))
grid = db.add(grid,m4e=exp(m4))
grid = db.add(grid,m5e=exp(m5))
grid = db.locate(grid,4,"z")
grid = db.indicator(grid,limits)
grid = db.add(grid,Permeability=pmax(1,m1e*Indicator.L.1+m2e*Indicator.L.2+m3e*Indicator.L.3+m4e*Indicator.L.4+m5e*Indicator.L.5))
grid = db.delete(grid,seq(5,19))
The resulting Porosity variable is represented graphically, together with the layer limits.
- Code: Select all
plot(grid,col=rg.colors(),name.image="Permeability")
plot(grid,name.contour=4,levels=c(0,1,2,3,4),add=T,lwd=2,col="yellow")
Now it is time to perpare the fluid propagation algorithm by defining a Facies variable (constantly set to 1) and a Fluid variable initiated to 0 except at the upper right corner of the grid where it is set to 1. Finally, we start the fluid propagation algorithm.
- Code: Select all
grid = db.add(grid,Facies=1)
grid = db.add(grid,Fluid=0)
grid[nx*ny,7] = 1
grid = fluid.propagation(grid,facies="Facies",fluid="Fluid",perm="Permeability",nfacies=1,nfluids=1)
The last part is the graphic representation of the propagation data together with the layer boundaries.
- Code: Select all
plot(grid,name.image="Fluid.Fill.Date",col=rg.colors(), title="Filling Date")
plot(grid,name.contour=4,levels=c(0,1,2,3,4),add=T,lwd=2,col="black")



